-
Примеры решений
- Алгебра
- Геометрия
- ОГЭ
-
ЕГЭ
- Базовый уровень
-
Профильный уровень
- Планиметрия
- Стереометрия
- Теория вероятностей ПРОФИЛЬ
- Простейшие уравнения
- График производной
- Расчет по формулам
- Текстовые задачи ПРОФИЛЬ
- Графики функций
- Наибольшее и наименьшее значения функции
- Точки максимума и минимума
- Уравнения повышенной сложности
- Стереометрия Часть 2 ЕГЭ
- Неравенства повышенной сложности
- Экономические задачи
- Задачи с параметром
- Векторы
- Темы задач
ОГЭ
Объемы
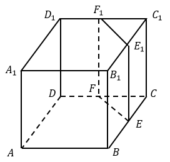
В кубе ABCDA1B1C1D1 все ребра равны 5. На его ребре ВВ1 отмечена точка К так, что КВ = 3. Через точки К и С1 проведена плоскость α, параллельная прямой BD1.
а) Докажите, что А1Р = РВ1 = 1 : 2, где Р - точка пересечения плоскости α с ребром A1B1.
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью α.
в) Найдите угол наклона плоскости α к плоскости грани ВВ1С1С.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания - точка С1, причем СС1 - образующая цилиндра, а АС - диаметр основания. Известно, что ∠АСВ = 30°, АВ = √2, СС1 = 2.
а) Докажите, что угол между прямыми АС1 и ВС равен 45°.
б) Найдите объем цилиндра.
в) Найдите расстояние от точки В до прямой АС1.
г) Найдите площадь боковой поверхности цилиндра.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания - точки В1 и С1, причем ВВ1 - образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите объем цилиндра, если АВ = 7, ВВ1 = 24, В1С1 = 10.
в) Найдите площадь боковой поверхности цилиндра.
г) Найдите угол между ВВ1 и АС1.
д) Найдите расстояние от точки В до прямой АС1.
Объем треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух ребер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объем куба.
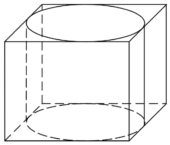
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объем параллелепипеда.