№ 23. Геометрия, готовые решения задач

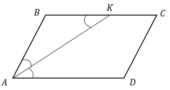
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК=10, СК=18.

Смотреть решение

108

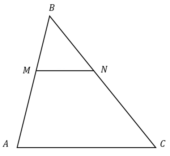
Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN=20, AC=35, NC=39.

Смотреть решение

139

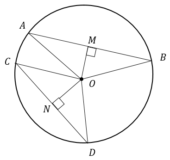
Отрезки АВ и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если АВ=20, CD=48, а расстояние от центра окружности до хорды АВ равно 24.

Смотреть решение

139

Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР=34, а сторона ВС в 2 раза меньше стороны АВ.

Смотреть решение

139

Высота АН ромба ABCD делит сторону CD на отрезки DH=20 и CH=5. Найдите высоту ромба.

Смотреть решение

131

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.

Смотреть решение

166

Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF=21, BF=20.

Смотреть решение

96

Точка Н является основанием высоты, проведенной из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если АН=4, АС=16.

Смотреть решение

110

ОГЭ

№ 23. Геометрия, готовые решения задач

ЕГЭ (базовый уровень)

ЕГЭ (профильный уровень)