Геометрия ОГЭ

Один из углов параллелограмма равен 127°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

Смотреть решение

570

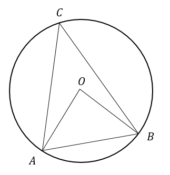
Треугольник АВС вписан в окружность с центром в точке О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 67°. Ответ дайте в градусах.

Смотреть решение

277

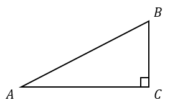
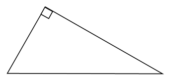
В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.

Смотреть решение

137

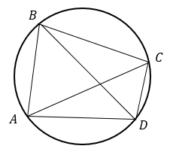
Четырехугольник ABCD вписан в окружность. Угол ABD равен 51°, угол CAD равен 42°. Найдите угол АВC. Ответ дайте в градусах.

Смотреть решение

316

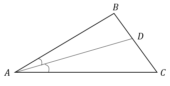
В треугольнике АВС известно, что ∠АВС=100°, ∠АСВ=52°, AD - биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Смотреть решение

1631

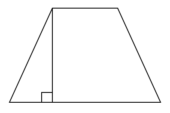
Основания трапеции равны 4 и 12, а высота равна 6. Найдите площадь этой трапеции.

Смотреть решение

220

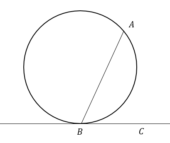
На окружности отмечены точки А и В так, что меньшая дуга АВ равна 152°. Прямая ВС касается окружности в точке В так, что угол АВС острый. Найдите угол АВС. Ответ дайте в градусах.

Смотреть решение

1235

В треугольнике АВС угол С равен 90°, ВС=14, АВ=20. Найдите cosB.

Смотреть решение

254

ОГЭ

Геометрия ОГЭ

ЕГЭ (базовый уровень)

ЕГЭ (профильный уровень)