-
Примеры решений
- Алгебра
- Геометрия
- ОГЭ
-
ЕГЭ
- Базовый уровень
-
Профильный уровень
- Планиметрия
- Стереометрия
- Теория вероятностей ПРОФИЛЬ
- Простейшие уравнения
- График производной
- Расчет по формулам
- Текстовые задачи ПРОФИЛЬ
- Графики функций
- Наибольшее и наименьшее значения функции
- Точки максимума и минимума
- Уравнения повышенной сложности
- Стереометрия Часть 2 ЕГЭ
- Неравенства повышенной сложности
- Экономические задачи
- Задачи с параметром
- Векторы
- Темы задач
ОГЭ
Касательные к окружности
На окружности отмечены точки А и В так, что меньшая дуга АВ равна 152°. Прямая ВС касается окружности в точке В так, что угол АВС острый. Найдите угол АВС. Ответ дайте в градусах.
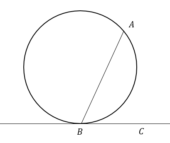
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ=2, АС=8.
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 3,6, а АВ=8.
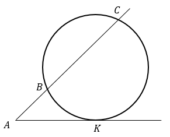
Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причем АВ = 4, АС = 64. Найдите АК.
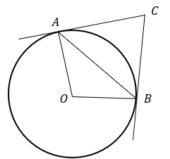
Касательные в точках А и В к окружности с центром в точке О пересекаются под углом 88°. Найдите угол АВО. Ответ дайте в градусах.