Прямоугольный треугольник

В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.

Смотреть решение

137

В треугольнике АВС угол С равен 90°, ВС=14, АВ=20. Найдите cosB.

Смотреть решение

250

В треугольнике АВС угол С равен 90°, sinB=4/15, АВ=45. Найдите АС.

Смотреть решение

1109

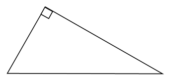
Точка Н является основанием высоты, проведенной из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если АН=4, АС=16.

Смотреть решение

110

Точка Н является основанием высоты ВН, проведенной из вершины прямоуго угла В прямоугольного треугольника АВС. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК=12.

Смотреть решение

124

Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе.

Смотреть решение

406

Сторона АС треугольника АВС проходит через центр описанной около него окружности. Найдите угол С, если ∠А = 33°. Ответ дайте в градусах.

Смотреть решение

334

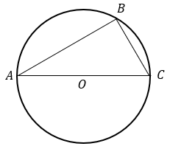
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если АС = 9.

Смотреть решение

549

ОГЭ

Прямоугольный треугольник

ЕГЭ (базовый уровень)

ЕГЭ (профильный уровень)