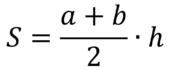-
Примеры решений
- Алгебра
- Геометрия
- ОГЭ
-
ЕГЭ
- Базовый уровень
-
Профильный уровень
- Планиметрия
- Стереометрия
- Теория вероятностей ПРОФИЛЬ
- Простейшие уравнения
- График производной
- Расчет по формулам
- Текстовые задачи ПРОФИЛЬ
- Графики функций
- Наибольшее и наименьшее значения функции
- Точки максимума и минимума
- Уравнения повышенной сложности
- Стереометрия Часть 2 ЕГЭ
- Неравенства повышенной сложности
- Экономические задачи
- Задачи с параметром
- Векторы
- Темы задач
ОГЭ
Расчет по формулам, готовые решения задач
Площадь треугольника можно вычислить по формуле S=abc/4R, где a, b и c - стороны треугольника, а R - радиус окружности, описанной около этого треугольника. Пользуясь этой формулой, найдите b, если а=12, с=13, S=30 и R=6,5.
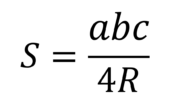
В фирме "Свежесть" стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С=9500+7200n, где n - число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 8 колец. Ответ дайте в рублях.

Мощность постоянного тока (в ваттах) вычисляется по формуле P=I2R, где I - сила тока (в амперах), R - сопротивление (в омах). Пользуясь этой формулой, найдите Р, если R=2 Ом и I=8,5 А.
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта пользуются формулой tF=1,8tC+32, где tC - температура в градусах Цельсия, tF - температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует -35 градусов по шкале Цельсия?
Перевести значение температуры по шкале Фаренгейта в шкалу Цельсия позволяет формула tC=5/9(tF-32), где tC - температура в градусах Цельсия, tF - температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 5 градусов по шкале Фаренгейта?
Площадь четырехугольника можно вычислить по формуле S=(d1d2sinα)/2, где d1 и d2 - длины диагоналей четырехугольника, α - угол между диагоналями. Пользуясь этой формулой, найдите длину d2, если d1=9, sinα=5/8, а S=56,25.
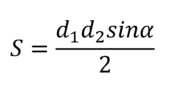
Сумма углов выпуклого многоугольника вычисляется по формуле E=(n-2)π, где n - количество его углов. Пользуясь этой формулой, найдите n, если Е=6π.
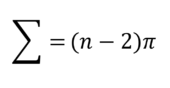
Площадь трапеции вычисляется по формуле S=((a+b)/2)·h, где а и b - длины оснований трапеции, h - ее высота. Пользуясь этой формулой, найдите площадь S, если а=6, b=4, h=6.