-
Примеры решений
- Алгебра
- Геометрия
- ОГЭ
-
ЕГЭ
- Базовый уровень
-
Профильный уровень
- Планиметрия
- Стереометрия
- Теория вероятностей ПРОФИЛЬ
- Простейшие уравнения
- График производной
- Расчет по формулам
- Текстовые задачи ПРОФИЛЬ
- Графики функций
- Наибольшее и наименьшее значения функции
- Точки максимума и минимума
- Уравнения повышенной сложности
- Стереометрия Часть 2 ЕГЭ
- Неравенства повышенной сложности
- Экономические задачи
- Задачи с параметром
- Векторы
- Темы задач
ОГЭ
Простейшие задачи (Ст), готовые решения задач
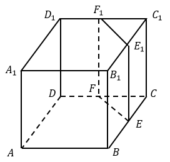
Объем треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух ребер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объем куба.
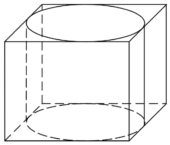
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объем параллелепипеда.